参考自
- 《机器学习》周志华
- 《南瓜书》
- 详解线性判别分析
- 使用ECOC编码提高多分类任务的性能
基本形式
给定由 $d$ 个属性描述的示例 $\boldsymbol{x}=(x^1,x^2,\cdots,x^d)^{\text{T}}$, 其中 $x^i$ 是 $\boldsymbol{x}$ 在第 $i$ 个属性上的取值, 线性模型 (linear model) 试图学得一个通过属性的线性组合来进行预测的函数, 即
\[f(\boldsymbol{x})=w_1x^1+w_2x^2+\cdots+w_dx^d+b\]用向量形式写出
\[f(\boldsymbol{x})=\boldsymbol{w}^{\text{T}}\boldsymbol{x}+b\]其中 $\boldsymbol{w}=(w_1,w_2,\cdots,w_d)^{\text{T}}$ 被称为权重 (weight), $b$ 被称为偏好 (bias).
线性模型形式简单, 易于建模. 由于 $\boldsymbol{w}$ 直观地表达了各属性在预测中的重要性, 因此线性模型有很好的可解释性 (comprehensibility).
这种可解释性体现在我们可以理解模型是如何作出预测结果的. 以后我们会看到, 这种性质在许多更为庞大复杂的模型面前显得更为可贵.
线性回归
给定数据集 \(D=\lbrace(\boldsymbol{x}_{1},y_{1}),(\boldsymbol{x}_{2},y_{2}),\cdots,(\boldsymbol{x}_{m},y_{m})\rbrace\), 其中 \(\boldsymbol{x}_{i}=\lbrace x_{i}^{1},x_{i}^{2},\cdots,x_{i}^{d}\rbrace, y_{i}\in \mathbb{R}\). 线性回归 (linear regression) 试图学得一个线性模型以尽可能准确地预测实值输出标记.
若属性值间存在”序” (order) 关系, 则可通过连续化将其转化成连续值. 若不存在序关系, 假定有 $k$ 个属性值, 则通常转化为 $k$ 维向量.
对于仅含一个属性的样本, 线性回归试图学得
\[f(x_i)=wx_i+b,\text{ 使得 }f(x_i)\simeq y_i.\]其中 $\simeq$ 表示相似或相等.
通过衡量 $f(x)$ 与 $y$ 之间的差别, 并让这种差别最小化, 可以确定 $w$ 和 $b$. 均方误差是回归任务中最常用的性能度量. 我们可试图让均方误差最小化
\[\begin{aligned} (w^{*},b^{*})& =\arg\min_{(w,b)}\sum_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2} \\ &=\arg\min_{(w,b)}\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^{2} \end{aligned}\]其中 $\arg\min\limits_{(w,b)}$ 意味使目标函数, 在此为 $\sum\limits_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2}$ 最小的 $(w,b)$ 取值.
均方误差对应了常用的欧几里得距离 (Euclidean distance). 基于均方误差最小化来进行模型求解的方法称为”最小二乘法” (least square method). 在线性回归中, 最小二乘法就是试图找到一条直线, 使所有样本到直线上的欧氏距离之和最小.
求解 $w$ 和 $b$ 使 $\displaystyle E_{(w,b)}=\sum_{i=1}^{m}(y_{i}-wx_{i}-b)^{2}$ 最小的过程称为线性回归模型的最小二乘”参数估计” (parameter estimation).
将 $E_{(w,b)}$ 分别对 $w$ 和 $b$ 求导得到
\[\begin{gathered} \frac{\partial E_{(w,b)}}{\partial w} =2\left(w\sum_{i=1}^mx_i^2-\sum_{i=1}^m\left(y_i-b\right)x_i\right) \\ \frac{\partial E_{(w,b)}}{\partial b} =2\left(mb-\sum_{i=1}^m\left(y_i-wx_i\right)\right), \end{gathered}\]令上述两式分别为 0 可得到 $w$ 和 $b$ 最优解的闭式 (closed-form) 解
\[\begin{aligned} w=\frac{\sum\limits_{i=1}^my_i(x_i-\bar{x})}{\sum\limits_{i=1}^mx_i^2-\frac{1}{m}\left(\sum\limits_{i=1}^mx_i\right)^2}, \end{aligned}\] \[b=\frac{1}{m}\sum_{i=1}^{m}(y_{i}-wx_{i}),\]其中 $\displaystyle\bar{x}=\frac{1}{m}\sum_{i=1}^{m}x_i$. 这里的”闭式解”又称”解析解”, 是指可以通过具体的表达式解出待解参数.
对于更一般的情形, 样本由 $d$ 个属性描述. 此时我们试图学得
\[f(\boldsymbol{x}_i)=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}_i+b,\text{ 使得 }f(\boldsymbol{x}_i)\simeq y_i,\]这称为”多元线性回归” (multivariate linear regression).
类似的, 可利用最小二乘法来对 $\boldsymbol{w}$ 和 $b$ 进行估计. 先把 $\boldsymbol{w}$ 和 $b$ 吸收入向量形式 $\hat{\boldsymbol{w}}=(\boldsymbol{w},b)^{\text{T}}$. 相应的, 把数据集 $D$ 表示为一个 $m\times (d+1)$ 大小的矩阵 $\mathbf{X}$, 其中每行对应于一个样本, 该行前 $d$ 个元素对应于样本的 $d$ 个属性值, 最后一个元素恒置为 1. 令 \(\hat{\boldsymbol{x}}_{i}=(x_{i}^{1},x_{i}^{2},\cdots,x_{i}^{d})^{\mathrm{T}}\).
\[\mathbf{X}=\begin{pmatrix}x_{1}^1&x_{1}^2&\ldots&x_{1}^d&1\\x_{2}^1&x_{2}^2&\ldots&x_{2}^d&1\\\vdots&\vdots&\ddots&\vdots&\vdots\\x_{m}^1&x_{m}^2&\ldots&x_{m}^d&1\end{pmatrix}=\begin{pmatrix}\boldsymbol{x}_1^\mathrm{T}&1\\\boldsymbol{x}_2^\mathrm{T}&1\\\vdots&\vdots\\\boldsymbol{x}_m^\mathrm{T}&1\end{pmatrix}=\begin{pmatrix}\hat{\boldsymbol{x}}_1^\mathrm{T}\\\hat{\boldsymbol{x}}_2^\mathrm{T}\\\vdots\\\hat{\boldsymbol{x}}_m^\mathrm{T}\end{pmatrix},\]将标记写成向量形式 $\boldsymbol{y}=(y_1,y_2,\cdots,y_m)^{\mathrm{T}}$, 可得
\[\begin{aligned} \hat{\boldsymbol{w}}^{*} & =\underset{\hat{\boldsymbol{w}}}{\operatorname{arg}\operatorname*{min}}\sum_{i=1}^{m}\left(y_{i}-\hat{\boldsymbol{w}}^{\mathrm{T}}\hat{\boldsymbol{x}}_{i}\right)^{2}\\ &=\underset{\hat{\boldsymbol{w}}}{\operatorname{arg}\operatorname*{min}}\sum_{i=1}^{m}\left(y_{i}-\hat{\boldsymbol{x}}_{i}^{\mathrm{T}}\hat{\boldsymbol{w}}\right)^{2}\\ &=\underset{\hat{\boldsymbol{w}}}{\operatorname{arg}\operatorname*{min}}\begin{bmatrix}y_1-\hat{\boldsymbol{x}}_1^\mathrm{T}\hat{\boldsymbol{w}}&\cdots&y_m-\hat{\boldsymbol{x}}_m^\mathrm{T}\hat{\boldsymbol{w}}\end{bmatrix}\begin{bmatrix}y_1-\hat{\boldsymbol{x}}_1^\mathrm{T}\hat{\boldsymbol{w}}\\\vdots\\y_m-\hat{\boldsymbol{x}}_m^\mathrm{T}\hat{\boldsymbol{w}}\end{bmatrix}\\ &=\underset{\hat{\boldsymbol{w}}}{\operatorname*{arg\min}}(y-\mathbf{X}\hat{\boldsymbol{w}})^\mathrm{T}(y-\mathbf{X}\hat{\boldsymbol{w}}) \end{aligned}\]令 $E_{\hat{\boldsymbol{w}}}=(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}})^\mathrm{T}(y-\mathbf{X}\hat{\boldsymbol{w}})$
\[\begin{aligned} E_{\hat{\boldsymbol{w}}}&=(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}})^\mathrm{T}(\boldsymbol{y}-\mathbf{X}\hat{\boldsymbol{w}})\\ &=\boldsymbol{y}^\mathrm{T}\boldsymbol{y}-\boldsymbol{y}^\mathrm{T}\boldsymbol{\mathrm{X}}\hat{\boldsymbol{w}}-\hat{\boldsymbol{w}}^\mathrm{T}\boldsymbol{\mathrm{X}}^\mathrm{T}\boldsymbol{y}+\hat{\boldsymbol{w}}^\mathrm{T}\boldsymbol{\mathrm{X}}^\mathrm{T}\mathrm{X}\hat{\boldsymbol{w}} \end{aligned}\]对 $\hat{\boldsymbol{w}}$ 求导得
\[\begin{aligned} \frac{\partial E_{\hat{\boldsymbol{w}}}}{\partial\hat{\boldsymbol{w}}}&=\frac{\partial\boldsymbol{y}^\mathrm{T}\boldsymbol{y}}{\partial\hat{\boldsymbol{w}}}-\frac{\partial\boldsymbol{y}^\mathrm{T}\mathbf{X}\hat{\boldsymbol{w}}}{\partial\hat{\boldsymbol{w}}}-\frac{\partial\hat{\boldsymbol{w}}^\mathrm{T}\mathbf{X}^\mathrm{T}\boldsymbol{y}}{\partial\hat{\boldsymbol{w}}}+\frac{\partial\hat{\boldsymbol{w}}^\mathrm{T}\mathbf{X}^\mathrm{T}\mathbf{X}\hat{\boldsymbol{w}}}{\partial\hat{\boldsymbol{w}}}\\ &=0-\mathbf{X}^\mathrm{T}\boldsymbol{y}-\mathbf{X}^\mathrm{T}\boldsymbol{y}+(\mathbf{X}^\mathrm{T}\mathbf{X}+\mathbf{X}^\mathrm{T}\mathbf{X})\hat{\boldsymbol{w}}\\ &=2\mathbf{ X}^{\mathrm{T}}\left(\mathbf{X}\hat{\boldsymbol{w}}-\boldsymbol{y}\right)\\ \end{aligned}\]令上式为 0 可得 $\hat{\boldsymbol{w}}$ 最优解的闭式解. 上式求导过程需了解矩阵微分原理与矩阵微分公式, 不熟悉的读者可以参考 机器学习中的数学(一): 矩阵微分.
当 $\mathbf{X}^\mathrm{T}\mathbf{X}$ 为满秩矩阵 (full-rank matrix) 或正定矩阵 (positive definite matrix) 时, 令上式为 0 可以得到
\[\hat{\boldsymbol{w}}^*=\left(\mathbf{X}^\mathrm{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathrm{T}\boldsymbol{y}\]则最终学得的多元线性回归模型为
\[f(\hat{\boldsymbol{x}}_i)=\hat{\boldsymbol{x}}_i^\mathrm{T}\left(\mathbf{X}^\mathrm{T}\mathbf{X}\right)^{-1}\mathbf{X}^\mathrm{T}\boldsymbol{y}.\]现实任务中 $\mathbf{X}^\mathrm{T}\mathbf{X}$ 往往不是满秩矩阵. 在许多任务中会遇到大量的变量, 数目甚至超过样例数, 导致 $\mathbf{X}$ 的列数多于行数, 于是 $\mathbf{X}^\mathrm{T}\mathbf{X}$ 不满秩, 从而能解出多个 $\hat{\boldsymbol{w}}$ . 选择哪一个解作为输出将由学习算法的归纳偏好决定, 常见的做法是引入正则化 (regularization) 项.
正则化项通常是在损失函数中加入的对模型参数的惩罚项, 用于对模型参数进行 $\hat{\boldsymbol{w}}$ 进行约束.
当我们希望线性模型的预测值逼近真实标记 $y$ 时, 就得到了线性回归模型. 也可以令线性模型的预测值逼近 $y$ 的衍生物. 假如我们认为示例所对应的输出标记是在指数尺度上变化, 那就可将输出标记的对数作为线性模型逼近的目标, 即
\[\ln y=\boldsymbol{w}^{\text{T}}\boldsymbol{x}+b\]上式就是”对数线性回归” (log-linear regression). 上式在形式上仍是线性回归, 实质上是在求取输入空间到输出空间的非线性函数映射.
考虑单调可微函数 $g(\cdot)$ , 令
\[g(y)=\boldsymbol{w}^{\text{T}}\boldsymbol{x}+b\]这样得到的模型称为”广义线性模型” (generalized linear model), 函数 $g(\cdot)$ 称为”联系函数” (link function). 对数线性回归的联系函数即为对数函数.
对数几率回归
对于分类任务, 由于输出空间是离散的, 若要运用线性模型, 则需要找到一个单调可微函数将分类任务的真是标记 $y$ 与线性回归模型的预测值联系起来.
考虑二分类任务, 输出标记 $y\in\lbrace0,1\rbrace$, 若要将实数值转换为 $\lbrace0,1\rbrace$, 最理想的联系函数是”单位阶跃函数” (unit-step function).
\[\left.y=\left\lbrace\begin{array}{cc}0,&z<0~;\\0.5,&z=0~;\\1,&z>0~,\end{array}\right.\right.\]预测值大于 0 就判为正例, 小于 0 就判为反例, 预测值为 0 则任意判别.
单位阶跃函数的问题是不连续, 我们要寻找的是单调可微函数. 单调可微这一性质的重要性将在后文体现.
于是需要在一定程度上近似单位阶跃函数的”替代函数” (surrogate function), 满足单调可微性质. 一个常用的替代函数是对数几率函数 (logistic function)
\[y=\frac{1}{1+\text{e}^{-z}}\]该函数是一种”Sigmoid 函数”. Sigmoid 函数是一种函数图像形似 S 的函数.
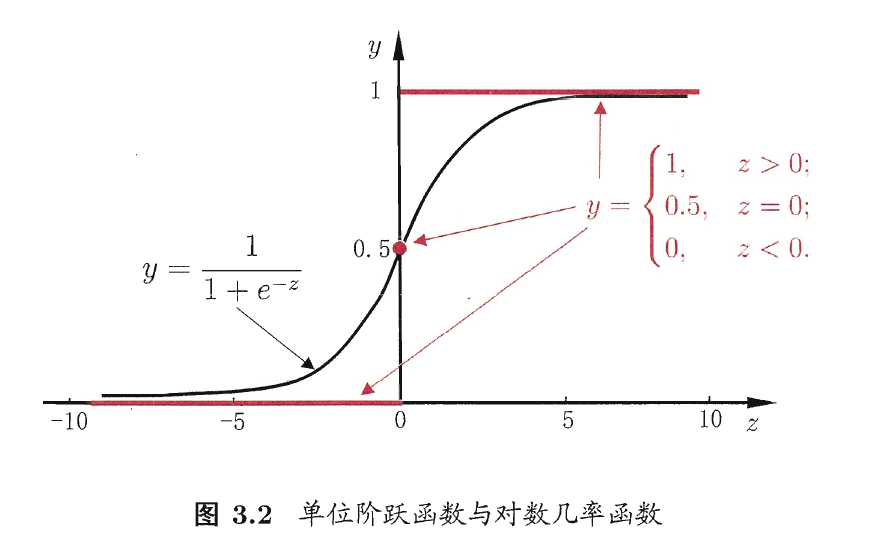
(上图来源于《机器学习》)
对数几率函数将预测值转换为一个处于 0 和 1 之间的实数值. 将对数几率函数作为替代函数得到下式
\[y=\frac{1}{1+\text{e}^{-(\boldsymbol{w}^{\text{T}}\boldsymbol{x}+b)}}\]上式可变化为
\[\ln\frac{y}{1-y}=\boldsymbol{w}^{\text{T}}\boldsymbol{x}+b\]可将 $y$ 视为样本 $\boldsymbol{x}$ 的作为正例的可能性, 则 $1-y$ 是作为反例的可能性, 二者的比值
\[\frac{y}{1-y}\]称为”几率” (odds), 反映了 $\boldsymbol{x}$ 作为正例的相对可能性. 对几率取对数则得到”对数几率” (log odds, 亦称 logit)
\[\ln\frac{y}{1-y}\]以上工作是在用线性回归模型的预测结果逼近真实标记的对数几率, 该模型称为”对数几率回归” (logistic regression). 这种方法有许多优点:
- 对分类可能性进行建模, 无需事先假设数据分布
- 可得到近似概率预测, 在一些任务中可用概率辅助决策
- 对数几率函数是任意阶可导的凸函数, 数学性质良好, 可应用许多数值优化算法
若将 $y$ 视为类后验概率估计 $p(y=1\vert x)$, 则可将上式重写为
\[\ln\frac{p(y=1\mid\boldsymbol{x})}{p(y=0\mid\boldsymbol{x})}=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b.\]由于 $p(y=0\vert x)=1-p(y=1\vert x)$, 可得
\[\begin{aligned} & p(y=1\mid\boldsymbol{x})=\frac{e^{\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b}}{1+e^{\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b}},\quad\\ &p(y=0\mid\boldsymbol{x})=\frac1{1+e^{\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b}}. \end{aligned}\]为便于讨论, 令 $\boldsymbol{\beta}=(\boldsymbol{w},b)^{\mathrm{T}}, \hat{\boldsymbol{x}}=(\boldsymbol{x},1)^{\mathrm{T}}$, 则将 $\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b$ 简写为 $\boldsymbol{\beta}^{\mathrm{T}}\hat{\boldsymbol{x}}$. 再令
\[\begin{aligned} &p_1(\hat{\boldsymbol{x}}; \boldsymbol{\beta})=p(y=1\mid\boldsymbol{x}; \boldsymbol{\beta}), \\ &p_0(\hat{\boldsymbol{x}}; \boldsymbol{\beta})=p(y=0\mid\boldsymbol{x}; \boldsymbol{\beta})=1-p_1(\hat{\boldsymbol{x}}; \boldsymbol{\beta}), \end{aligned}\]由于 $y\in\lbrace0,1\rbrace$, 则
\[p(y)=yp_1(\hat{\boldsymbol{x}}; \boldsymbol{\beta})+(1-y)p_0(\hat{\boldsymbol{x}}; \boldsymbol{\beta})\]接下来可以使用”极大似然法” (maximum likelihood method) 来估计 $\boldsymbol{w}$ 和 $b$. 即给定数据集 \(\lbrace(\boldsymbol{x}_{i},y_{i})\rbrace_{i=1}^{m}\), 要使以下函数
\[\ell(\boldsymbol{\beta})=\sum_{i=1}^m\ln\left(y_ip_1(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta})+(1-y_i)p_0(\hat{\boldsymbol{x}}_i;\boldsymbol{\beta})\right)\]最大化.
上式是关于 $\boldsymbol{\beta}$ 的高阶可导连续凸函数, 可用梯度下降法 (gradient descent) 和牛顿法 (Newton method) 等经典数值优化算法来求其最优解. 梯度下降法与牛顿法在此不展开, 将在其他文章中详细介绍.
《机器学习》原书中写了”将 $y$ 视为类后验概率估计 $p(y=1\vert x)$” 后, 就说明要用最大似然估计 (Maximum Likelihood Estimation, MLE) 来估计参数值. 而笔者了解到, 后验概率估计对应的方法似乎应是最大后验概率估计 (Maximum A Posteriori Estimation, MAE), 书中给出似然函数后, 似乎又将条件概率密度函数简化为普通的概率密度函数. 故笔者认为这是为了方便讨论而作出的简化. 于是在笔记中重新编排了讲述顺序.
线性判别分析
线性判别分析 (Linear Discriminant Analysis, LDA) 是一种线性学习方法, 其思想是: 给定训练样例集, 设法将样例投影到一条直线上, 使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离; 在对新样本进行分类时, 将其投影到同样的这条直线上, 再根据投影点的位置来确定新样本的类别.
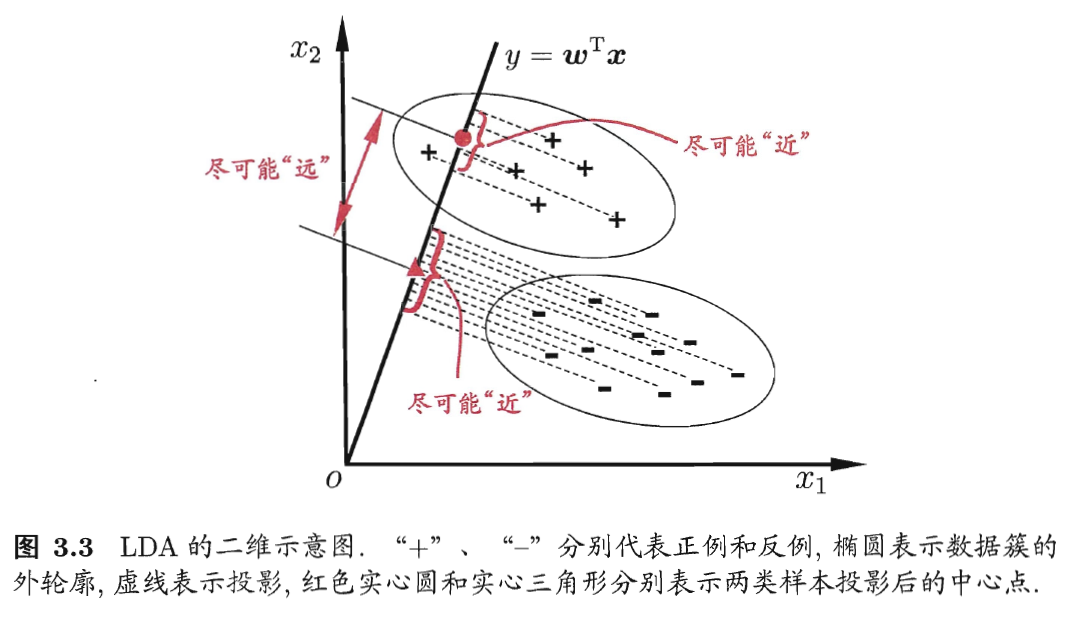
(上图来源于《机器学习》)
上图中的直线 $y=\boldsymbol{w}^{\text{T}}\boldsymbol{x}$ 就是要学得的模型
给定数据集 \(D=\lbrace(\boldsymbol{x}_{i},y_{i})\rbrace_{i=1}^{m},y_{i}\in\lbrace0,1\rbrace\), 令 \(X_i\) 表示第 \(i\in\lbrace0,1\rbrace\) 类示例的集合, \(\boldsymbol{\mu}_i\) 表示第 $i\in\lbrace0,1\rbrace$ 类示例的均值向量, 假设每个样本有 \(n\) 个属性
\[\displaystyle \boldsymbol{\mu}_i^k=\left[\frac{1}{m}\sum_{x_i\in X_i}x_{i}^{1},\cdots,\frac{1}{m}\sum_{x_i\in X_i}x_{i}^{n}\right]^{\text{T}}\]根据向量内积的几何性质, 若要将数据投影到直线 $\boldsymbol{w}$ 上, 则要将样本点与 $\boldsymbol{w}$ 作内积. 两类样本的中心在直线上的投影分别为 $\boldsymbol{w}^{\text{T}}\boldsymbol{\mu}_0$ 和 $\boldsymbol{w}^{\text{T}}\boldsymbol{\mu}_1$. 由于直线是一维空间, 故 $\boldsymbol{w}^{\text{T}}\boldsymbol{\mu}_0$ 和 $\boldsymbol{w}^{\text{T}}\boldsymbol{\mu}_1$ 都是实数. 两类样本中心之间的距离可表示为
\[\|\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_1\|_2^2\]即两个中心之间的欧几里得距离.
令 $\mathbf{\Sigma}_{i}$ 表示第 $i\in\lbrace0,1\rbrace$ 类示例的协方差矩阵, 即
\[\mathbf{\Sigma}_{i}=\sum_{\boldsymbol{x}\in X_i}(\boldsymbol{x}-\boldsymbol{\mu}_0)(\boldsymbol{x}-\boldsymbol{\mu}_0)^\text{T}\]我们可以计算两类示例投影到直线 $\boldsymbol{w}$ 上的点的协方差矩阵
\[\sum_{\boldsymbol{x}\in X_i}(\boldsymbol{w}^\mathrm{T}\boldsymbol{x}-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0)(\boldsymbol{w}^\mathrm{T}\boldsymbol{x}-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0)^\text{T}=\boldsymbol{w}^\mathrm{T}\mathbf{\Sigma}_{i}\boldsymbol{w}\]$\boldsymbol{w}^\mathrm{T}\mathbf{\Sigma}_{i}\boldsymbol{w}$ 也是实数.
欲使同类样例的投影点尽可能接近, 可以让同类样例投影点的协方差尽可能小, 即 \(\boldsymbol{w}^\mathrm{T}\mathbf{\Sigma}_{0}\boldsymbol{w}+\boldsymbol{w}^\mathrm{T}\mathbf{\Sigma}_{1}\boldsymbol{w}\) 尽可能小; 欲使异类样例的投影点尽可能远离, 可以让类中心之间的距离尽可能大, 即 \(\|\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_1\|_2^2\) 尽可能大, 同时考虑二者即得到最大化的目标为
\[\begin{aligned} J& =\frac{\|\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_0-\boldsymbol{w}^\mathrm{T}\boldsymbol{\mu}_1\|_2^2}{\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_0\boldsymbol{w}+\boldsymbol{w}^\mathrm{T}\boldsymbol{\Sigma}_1\boldsymbol{w}} \\ &=\frac{\boldsymbol{w^\mathrm{T}}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)^\mathrm{T}\boldsymbol{w}}{\boldsymbol{w^\mathrm{T}}(\boldsymbol{\Sigma}_0+\boldsymbol{\Sigma}_1)\boldsymbol{w}}. \end{aligned}\]定义”类内散度矩阵” (within-class scatter matrix)
\[\begin{aligned}\mathbf{S}_w&=\mathbf{\Sigma}_0+\mathbf{\Sigma}_1\\&=\sum_{\boldsymbol{x}\in X_0}\left(\boldsymbol{x}-\boldsymbol{\mu}_0\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_0\right)^\mathrm{T}+\sum_{\boldsymbol{x}\in X_1}\left(\boldsymbol{x}-\boldsymbol{\mu}_1\right)\left(\boldsymbol{x}-\boldsymbol{\mu}_1\right)^\mathrm{T}\end{aligned}\]以及”类间散度矩阵” (between-class scatter matrix)
\[\mathbf{S}_b=\left(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\right)\left(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1\right)^\mathrm{T}\]于是 $J$ 可重写为
\[J=\frac{\boldsymbol{w}^\mathrm{T}\mathbf{S}_b\boldsymbol{w}}{\boldsymbol{w}^\mathrm{T}\mathbf{S}_w\boldsymbol{w}}\]这就是 LDA 欲最大化的目标.
类内散度矩阵用于衡量同一类别内样本之间的相似性, 类间散度矩阵是用于衡量不同类别之间样本的差异性.
注意到上式的分子分母都是 $\boldsymbol{w}$ 的二次项, 因此上式的解与 $\boldsymbol{w}$ 的大小无关, 只与 $\boldsymbol{w}$ 的方向有关. 可类比如下形式的函数
\[\frac{a_{1}\omega_{1}^{2}+a_{2}\omega_{1}\omega_{2}+a_{3}\omega_{2}^{2}}{b_{1}\omega_{1}^{2}+b_{2}\omega_{1}\omega_{2}+b_{3}\omega_{2}^{2}}=\frac{a_1+a_2\frac{\omega_2}{\omega_1}+a_3(\frac{\omega_2}{\omega_1})^2}{b_1+b_2\frac{\omega_2}{\omega_1}+b_3(\frac{\omega_2}{\omega_1})^2}\]不失一般性, 令 $\boldsymbol{w}^\mathrm{T}\mathbf{S}_w\boldsymbol{w}=1$, 则优化的目标变成
\[\min-\boldsymbol{w}^\mathrm{T}\mathbf{S}_b\boldsymbol{w}\]由上式, 定义拉格朗日函数
\[L(\boldsymbol{w},\lambda)=-\boldsymbol{w}^\mathrm{T}\mathrm{S}_b\boldsymbol{w}+\lambda(\boldsymbol{w}^\mathrm{T}\mathrm{S}_w\boldsymbol{w}-1)\]对 $\boldsymbol{w}$ 求偏导可得
\[\begin{aligned} \begin{aligned}\frac{\partial L(\boldsymbol{w},\lambda)}{\partial \boldsymbol{w}}\end{aligned}& \begin{aligned}=-\frac{\partial(\boldsymbol{w^\mathrm{T}}\mathbf{S}_b\boldsymbol{w})}{\partial\boldsymbol{w}}+\lambda\frac{\partial(\boldsymbol{w^\mathrm{T}}\mathbf{S}_w\boldsymbol{w}-1)}{\partial\boldsymbol{w}}\end{aligned} \\ &=-(\mathbf{S}_b+\mathbf{S}_b^\mathrm{T})\boldsymbol{w}+\lambda(\mathbf{S}_w+\mathbf{S}_w^\mathrm{T})\boldsymbol{w} \end{aligned}\]由于 $\mathbf{S}_b=\mathbf{S}_b^\mathrm{T},\mathbf{S}_w=\mathbf{S}_w^\mathrm{T}$
\[\frac{\partial L(\boldsymbol{w},\lambda)}{\partial\boldsymbol{w}}=-2\mathbf{S}_b\boldsymbol{w}+2\lambda\mathbf{S}_w\boldsymbol{w}\]令上式等于 0 即可得
\[\begin{aligned} -2\mathbf{S}_b\boldsymbol{w}+2\lambda\mathbf{S}_w\boldsymbol{w}&=0\\ \mathbf{S}_b\boldsymbol{w}&=\lambda\mathbf{S}_w\boldsymbol{w}\\ (\boldsymbol{\mu}_0-\boldsymbol{\mu}_1))(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1))^\mathrm{T}\boldsymbol{w}&=\lambda\mathbf{S}_w\boldsymbol{w} \end{aligned}\]若令 $(\mu_0-\mu_1)^\mathrm{T}\boldsymbol{w}=\gamma$ 则有
\[\begin{aligned}\gamma(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)&=\lambda\mathbf{S}_w\boldsymbol{w}\\\boldsymbol{w}&=\frac\gamma\lambda\mathbf{S}_w^{-1}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)\end{aligned}\]由于只关心 $\boldsymbol{w}$ 的方向, 而不关心其取值, 而 $\gamma$ 的大小取决于 $\boldsymbol{w}$, 因此可以让 $\boldsymbol{w}$ 任意取值使得 $\gamma=\lambda$. 此时求解出 $\boldsymbol{w}$
\[\boldsymbol{w}=\mathbf{S}_w^{-1}(\boldsymbol{\mu}_0-\boldsymbol{\mu}_1)\]可以将 LDA 推广到多分类任务中. LDA 同时也是一个常用的降维方法. 虽然书中有所介绍, 但 LDA 的思想丰富, 便不在此展开了. 感兴趣的朋友可以参考 LDA-线性判别分析(三)推广到 Multi-classes 情形. 感谢各位大佬的辛勤写作与无私分享.
多分类学习
对于多分类问题, 可以基于一些基本策略, 利用二分类模型解决多分类问题.
考虑 $N$ 个类别 $C_1,C_2,\cdots,C_n$, 多分类学习的基本思路是”拆解法”, 即将多分类任务拆为若干个二分类任务求解. 具体来说, 先对问题进行拆分, 然后为拆出的每个二分类任务训练一个分类器; 在测试时, 对这些分类器的预测结果进行集成以获得最终的多分类结果.
经典的拆分策略有三种:
- 一对一 (One vs. One, OvO)
- 一对多 (One vs. Rest, OvR)
- 多对多 (Many vs. Many, MvM)
给定数据集 $D=\lbrace(\boldsymbol{x}_1,y_1),(\boldsymbol{x}_2,y_2),\ldots,(\boldsymbol{x}_m,y_m)\rbrace,y_i\in\lbrace C_1,C_2,\ldots,C_N\rbrace.$
OvO 将这 $N$ 个类别两两配对, 产生 $N(N-1)/2$ 个二分类任务. 在测试阶段, 新样本将同时提交给所有分类器, 得到 $N(N-1)/2$ 个分类结果, 最终结果可通过投票产生.
OvR 每次将一个类的样例作为正例, 其他所有类的样例作为反例来训练 $N$ 个分类器. 在测试时若仅有一个分类器预测为正类 , 则对应的类别标记为最终分类结果. 若有多个分类器预测为正类, 通常考虑各个分类器的预测置信度, 选择置信度最大的类别标记作为分类结果.
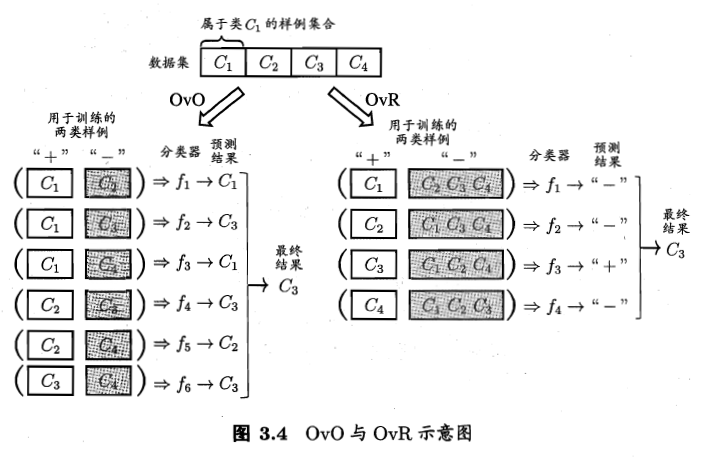
(上图来源于《机器学习》)
MvM 是每次将若干个类作为正类, 若干个其他类作为反类. MvM 的正、反类需要特殊的设计.
“纠错输出码” (Error Correcting Output Codes, ECOC) 是一种常用的 MvM 技术, 它将编码的思想引入类别拆分, ECOC 工作过程主要分两步.
- 编码: 对 N 个类别做 M 次划分, 每次划分将一部分类别划为正类, 一部分划为反类, 从而形成一个二分类训练集; 这样一共产生 M 个训练集, 可以训练出 M 个分类器.
- 解码: M 个分类器分别对测试样本进行预测, 这些预测标记组成一个编码, 将这个预测编码与每个类别各自的编码进行比较, 返回其中距离最小的类别作为最终预测结果.
类别划分通过”编码矩阵” (coding matrix) 指定. 编码矩阵有多种形式, 常见的主要有二元码与三元码. 二元码将每个类别指定为正类和反类. 三元码将每个类别分别制定为正类, 反类和”停用类”. 如下图所示
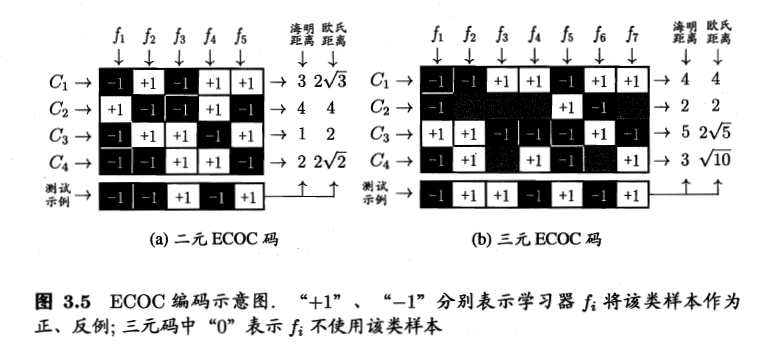
(上图来源于《机器学习》)
在编码阶段, 我们给予每个类别具有特定维度的、各自特殊的编码, 如上图 (a) 中 $C_1$ 的编码为 $(-1,+1,-1,+1,+1)$, $C_3$ 的编码为 $(-1,+1,+1,-1,+1)$. 编码的维度由我们自行决定, 而维度也决定了需要训练的二分类器的数量, 如 (a) 需要训练 5 个分类器, (b) 需要训练 7 个分类器.
在解码阶段, 各个分类器的预测结果联合起来形成了测试示例的编码. 将该编码与各类所对应的编码进行比较, 将距离最小的编码所对应的类别作为预测结果. 图 (a), 测试示例的编码为 $(-1,-1,+1,-1,+1)$, 其中”海明距离” (Hamming Distance) 指的是两组编码之间对应位置不相同的个数, 测试示例的编码与 $C_1$ 的编码有三个不同, 于是其海明距离为 3. 其中”欧式距离”指的就是将两组编码视为向量后, 计算两个向量的欧几里得距离. 测试示例与 $C_1$ 的欧氏距离为 $\sqrt{(-1-(-1))^2+(-1-1)^2+(1-(-1))^2+(-1-1)^2+(1-1)^2}=2\sqrt{3}$. 对于图 (b) 中的”停用类”, 计算时算作 0.5.
ECOC 编码对分类器的错误具有一定的容忍与修正能力. 图 (a) 中测试示例的正确预测编码是 $(-1,+1,+1,-1,+1)$, 假设在预测时某个分类器出错了, 例如 $f_2$ 出错从而导致错误编码 $(-1,-1,+1,-1,+1)$, 但基于这个编码仍能产生正确的最终分类结果 $C_3$.
一般来说, 对于同一个学习任务, ECOC 编码越长, 纠错能力越强, 但这也意味着所需训练的分类器越多.
类别不平衡问题
如果在训练分类器的过程中, 不同类别的训练样例数目差别很大, 则会对模型训练造成困扰.
类别不平衡 (class-imbalance) 就是指分类任务中不同类别的训练样例数目差别很大的情况.
当我们使用线性分类器 $y=\boldsymbol{w}^\mathrm{T}\boldsymbol{x}+b$ 对新样本 $\boldsymbol{x}$ 进行分类时, 事实上是在用预测出的 $y$ 值与一个阈值作比较, 通常在 $y>0.5$ 时判别为正例, 否则为反例. $y$ 实际上表达了正例的可能性, 几率 $y/(1-y)$ 则反映了正例可能性于反例可能性之比值. 阈值设置为 $0.5$ 恰表明分类器任务真实正、反例可能性相同.
然而当训练集中正、反例的数目不同时, 令 $m^+$ 表示正例数目, $m^-$ 表示反例数目, 则观测几率是 $m^+/m^-$, 由于我们通常假设训练集是真是总体样本的无偏采样, 因此观测几率就代表了真实几率. 于是, 只要分类器的预测几率高于观测几率就应判为正例, 即
\[\text{若 }\frac{y}{1-y}>\frac{m^{+}}{m^{-}}\text{则 预测为正例}.\]但是, 我们的分类器是基于下式进行决策的.
\[\text{若 }\frac{y}{1-y}>1\text{则 预测为正例}.\]因此, 需要对预测值进行调整, 只需令
\[\frac{y'}{1-y'}=\frac{y}{1-y}\times\frac{m^-}{m^+}.\]这就是类别不平衡学习的一个基本策略, “再缩放” (rescaling).
再缩放的策略中假设了训练集是真实样本总体的无偏采样. 这个假设往往并不成立. 对于类别不平衡的问题, 现有技术大体上有三类做法:
- 欠采样 (undersampling): 去除训练集比例较大的类别, 使得正、反例数目接近
- 过采样 (oversampling): 增加训练集中比例较小的类别
- 阈值移动 (threshold-moving): 类似再缩放策略